모달창 닫기
- 홈으로 이동
항성의 내부 구조
내부평형조건별의 내부로 향하려는 중력과 밖으로 향하려는 압력에 의한 힘이 내부의 모든 점(r)에서 완전히 평형을 이룰 때 이 별은 정유체역학적 평형이 이루어진다. 이 상태의 별은 더 이상 수축하거나 팽창하지 않는 안정적인 상태에 있게 된다. 만약 내부로 향하려는 중력이 더 크다면 별은 수축할 것이고 밖으로 향하려는 압력이 크다면 별은 팽창하게 된다.
별이 정유체역학적 평형을 이루고 있으면, 어떤 물체가 중심으로 접근할수록 그 위에 놓인 물체 무게의 증가와 대등하게 압력도 계속 증가해야한다. 따라서
별이 정유체역학적 평형을 이루고 있으면, 어떤 물체가 중심으로 접근할수록 그 위에 놓인 물체 무게의 증가와 대등하게 압력도 계속 증가해야한다. 따라서
으로 나타낼 수 있다.
위 식에서 3개의 독립변주 압력분포 P(r), 밀도 ρ(r), 질량 M(r)있는데, M(r)의 경우 구형의 껍질이 첨가될 때 (r에서 r+dr까지),
위 식에서 3개의 독립변주 압력분포 P(r), 밀도 ρ(r), 질량 M(r)있는데, M(r)의 경우 구형의 껍질이 첨가될 때 (r에서 r+dr까지),
만큼 증가한다. 따라서 M(r)은 ρ(r)로부터,
로 구할 수 있다.
별의 반지름을 R이라 하면, 별의 총 질량은
별의 반지름을 R이라 하면, 별의 총 질량은
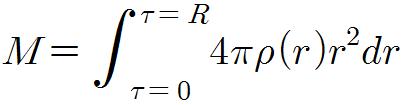
이다. 이것은 단순히 양파와 같은 껍질의 질량을 모두 합한 것이다. 따라서 질량 M(r)과 별 내부에서의 압력 분포 P(r)를 결정하기 위해서는 밀도 ρ(r)를 알아야 한다. 그리고 반지름 R을 구하면 마지막 식을 이용해 질량 M을 구할 수 있다.
항성의 에너지원
별이 빛을 내기위해서는 그만큼의 에너지 손실이 있어야 한다. 또한 계속해서 빛을 내기 위해서는 에너지 손실비와 같은 양의 에너지를 생성해야 한다. 즉, 열적 평형을 이루어야 한다는 것이다. 가스로 이루어진 별에서 에너지는 보통 중력수축과 열핵융합 반응에 의해서 생성된다.
중력 수축
별 내부의 가스와 티끌 입자들은 각각 운동을 하고 있지만 서로의 인력 때문에 전체적으로 안쪽으로 수축하게 되는데 이를 중력 수축이라 한다. 중력의 위치 에너지는 운동 에너지로 전환될 수 있는데 운동 에너지의 한 형태가 열이다. 매우 천천히 수축하고 있는 별을 가정해 보면, 내부의 열에너지는 그 별의 중력에 맞서 별을 지탱하는 압력을 준다. 이때의 압력은 가스 입자의 무질서한 운동 때문에 발생한다. 별의 반지름이 점점 작아지면 별 내부의 중력은 증가하게 된다. 따라서 내부의 압력 또한 정유체역학적 평형을 유지하기 위해 증가된다. 하지만 중력 위치 에너지는 열에너지 증가량의 약 2배의 속도로 빨리 감소하는데 이 계의 총 에너지는 보존 되어야 함으로 위치 에너지의 약 절반이 공간으로 복사 되어야 한다. 이것이 별의 광도로 나타나는 것이다.
태양은 중력 수축만으로는 현재의 광도로 1500만년 동안밖에 유지하지 못한다. 따라서 태양이 수십억 년 동안 빛나고 있는 것을 설명하기 위해서는 다른 에너지원이 필요하다.
열핵반응
태양은 중력 수축만으로는 현재의 광도로 1500만년 동안밖에 유지하지 못한다. 따라서 태양이 수십억 년 동안 빛나고 있는 것을 설명하기 위해서는 다른 에너지원이 필요하다.
1938년 이후 천문학자들은 오래 지속되는 별의 에너지원이 열핵융합 반응임을 밝혀냈다. 이핵융합반응은 가벼운 원자핵이 고온 고밀도의 항성 내부에서 자주 격렬하게 충돌하여 더 무거운 핵으로 합쳐져 매운 큰 양의 에너지를 방출하는 것이다.
별은 수소의 함량비가 크기 때문에 별의 핵반응에서는 수소가 주요 성분이다. 수소핵(양성자)은 원자량이 1이므로 4개의 양성자가 모여 1개의 헬륨핵을 만든다. 하지만 수소 4개의 원자량과 헬륨 1개의 원자량은 정확하게 일치하지 않는다. 수소핵의 정확한 원자량은 1.0078이고 이것의 4개는 4.0312인 반면, 헬륨의 원자량은 4.0026이므로 0.0286의 질량손실이 생긴다. 이를 아인슈타인의 질량-에너지 등가 방정식(E=mc2)로 보면, (c: 광속, 원자량m: 1.66×10-17kg) 수소핵 4개가 헬륨으로 전환될 때 방출되는 에너지는,
E=0.0286(1.66×10-17)(9×1016)=4.3×10-12J
이다.
수소에서 헬륨으로 전환되는 방법에는 양성자-양성자 연쇄 반응(P-P chain)과 탄소 순환 반응(CNO cycle)이 있다. 낮은 온도에서는 P-P 연쇄 반응이 우세하며, 높은 온도에서는 CNO 순환 반응이 더 활발히 일어난다.
별은 수소의 함량비가 크기 때문에 별의 핵반응에서는 수소가 주요 성분이다. 수소핵(양성자)은 원자량이 1이므로 4개의 양성자가 모여 1개의 헬륨핵을 만든다. 하지만 수소 4개의 원자량과 헬륨 1개의 원자량은 정확하게 일치하지 않는다. 수소핵의 정확한 원자량은 1.0078이고 이것의 4개는 4.0312인 반면, 헬륨의 원자량은 4.0026이므로 0.0286의 질량손실이 생긴다. 이를 아인슈타인의 질량-에너지 등가 방정식(E=mc2)로 보면, (c: 광속, 원자량m: 1.66×10-17kg) 수소핵 4개가 헬륨으로 전환될 때 방출되는 에너지는,
E=0.0286(1.66×10-17)(9×1016)=4.3×10-12J
수소에서 헬륨으로 전환되는 방법에는 양성자-양성자 연쇄 반응(P-P chain)과 탄소 순환 반응(CNO cycle)이 있다. 낮은 온도에서는 P-P 연쇄 반응이 우세하며, 높은 온도에서는 CNO 순환 반응이 더 활발히 일어난다.
항성모형
별 구조의 기본적인 원리는 정유체역학적 평형, 이상 기체의 상태 방정식, 여러 가지 에너지 전달 방식, 별과 에너지의 중력 수축 과 열핵반응에 관한 식으로 나타낼 수 있다. 이 식들은 별의 모형(이론적인 별)을 계산할 때 사용되며, 온도 T(r), 질량 M(r), 밀도 ρ(r), 압력 P(r), 광도 L(r), 에너지 생성률 ε(r)와 평균 분자량 μ(r)로 표기된다.
정유체 역학적 평형
이 방정식들을 통하여 중심이나 표면과 같이 별의 어떤 한 점에서의 값을 알고 있다면 별 전체를 통하여 인수가 어떻게 변하는 지를 설명할 수 있다.
최종수정일
2017년 3월 31일

