모달창 닫기
- 홈으로 이동
공전
공전궤도를 이용한 행성의 거리 구하기
행성의 공전주기를 알면 케플러 제 3법칙을 사용하여 행성의 거리를 알 수 있다. 케플러 제3법칙은 행성의 거리와 공전주기와의 관계를 나타내는데 거리의 세제곱은 공전주기의 제곱과 같다는 것을 보여준다. 그리고 이러한 거리는 태양과 지구사이를 기준으로 한 천문단위(Astronomical Unit, AU)를 단위로 사용한다.
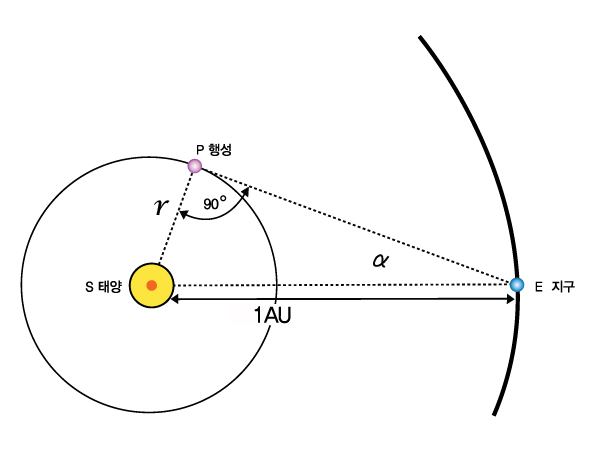행성의 거리를 구할 때는 내행성과 외행성을 나누어 구해야 한다. 태양과 내행성의 거리 r은 내행성이 최대 이각을 이룰 때 얻을 수 있다. S를 태양, E를 지구라 하고 P가 내행성이 최대 이각을 이룰 때의 점이라고 한다면, 거리 SE는 1AU(1억5천만km)가 되고 각 EPS는 90도가 된다. 따라서 각 SEP를 α로 하면 삼각법에 의해
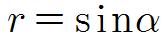
라 할 수 있다. 이 방법은 코페르니쿠스가 처음 사용하였다고 한다.
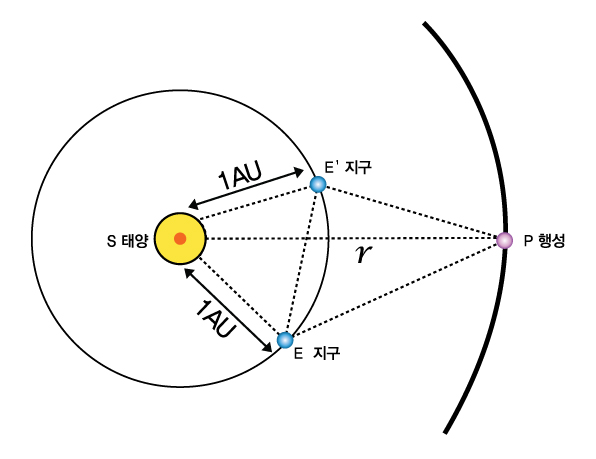
외행성의 거리를 구하는 방법은 내행성의 방법보다 복잡한데, 외행성의 1항성 주기의 시작과 끝을 P라고 하면 그때의 지구의 위치는 각각 E, E'에 있다. 여기서 우리는 행성의 주기를 알고 있으므로 각 ESE'를 알 수 있고, 각 PES와 각 PE'S는 관측을 해야 한다. 따라서 우리는 코사인 법칙과 삼각법을 이용하여 EE'의 거리와 각 SEE', 각 SEE'를 구할 수 있다. 구해진 값을 이용해 각 PEE'와 각 PE'E가 구해지므로 △EPE'의 값들을 풀 수 있고, △SEP나 △SE'P를 이용해 거리 r를 구할 수 있다.
이 방법은 케플러가 처음으로 화성의 궤도를 그려 그것이 타원임을 알아내는데 썼던 것으로 행성의 원 궤도에 대한 천문학의 전통을 깨뜨린 중요한 사건이다.
이 방법은 케플러가 처음으로 화성의 궤도를 그려 그것이 타원임을 알아내는데 썼던 것으로 행성의 원 궤도에 대한 천문학의 전통을 깨뜨린 중요한 사건이다.
최종수정일
2020년 11월 16일