모달창 닫기
- 홈으로 이동
전자기 복사
원자구조원자는 원자핵과 그 주위를 도는 전자들로 이루어진 것으로 20세기 초에 영국의 러더퍼드(Daniel Rutherford)의 실험과 보어(Niels Bohr)의 양자 가설 등에 의하여 처음 밝혀졌다. 그 후, 수십 년간 수많은 물리학자들에 의해 양자역학 및 원자핵 물리학이 많은 발전을 이뤘었고, 오늘날에는 원자핵의 구조를 상당한 수준까지 이해하기에 이르렀다. 원자핵은 전기적으로 양성인 양성자와 중성인 중성자들의 모임으로 이루어져 있으며, 이러한 모임을 '핵자'라고 부른다. 단, 원자번호가 1인 수소는 하나의 양성자만으로 핵을 이루고 있으며 그 주위를 하나의 전자가 돌고 있다고 생각하고 있다. 원자번호가 2인 헬륨은 하나의 양성자와 하나의 중성자가 원자핵을 이루며 그 주위를 전자 두 개가 돌고 있다. 원자번호가 12인 탄소의 경우, 각각 6개씩의 양성자와 중성자가 핵자를 이루고 있으며 가장 안정된 구조로서 12개의 전자가 그 주위를 돌고 있다. 위에 경우는 모두 같은 수의 양성자 수와 전자 수를 가지므로 원자는 전기적으로 중성이며, 일반적으로 이러한 경우의 원자핵이 안정된 핵이라 할 수 있다. 수소의 경우 중성자를 하나 또는 두 개씩 가질 수도 있는데 이들을 각각 중수소(2H) 및 삼중수소(3H)라고 하고, 이를 수소의 동위원소라고 한다. 다른 원소들도 물론 동위원소들을 가진다. 예를 들면, 헬륨은 각각 2개씩의 중성자와 전자들을 가졌으나 단 하나의 양성자를 가진 동위원소(3He)도 존재한다. 양성자의 질량은 약 1.6726×10-27kg이며 중성자의 질량과 거의 비슷하다. 이는 전자가 양성자 질량의 약 1/1840 정도이기 때문에 나타나는 현상이다. 따라서 양성자와 전자로 이루어진 수소 원자의 경우 그 질량은 거의 양성자 질량과 같다.
원자핵과 전자의 거리는 약 5×10-10m인 반면에 핵자의 양성자와 중성자 사이의 거리는 그 보다 수만 배 작은 약 10-15m(1 fm, 'femto-meter')이다. 이와 같이 상대적으로 거리가 먼 원자핵과 전자 간에는 양성자들과 전자들 간의 전기력이 작용한다. 반면에 1 fm이내의 짧은 거리에서는 양성자와 중성자간에 '중간자'(meson)라는 것이 매개하는 강한 핵력이 작용한다. 1934년 일본의 유카와 히데키(Hideki Yukawa)는 중간자의 존재를 이론적으로 유도하여 1949년 노벨 물리학상을 수상하였다.
원자핵과 전자의 거리는 약 5×10-10m인 반면에 핵자의 양성자와 중성자 사이의 거리는 그 보다 수만 배 작은 약 10-15m(1 fm, 'femto-meter')이다. 이와 같이 상대적으로 거리가 먼 원자핵과 전자 간에는 양성자들과 전자들 간의 전기력이 작용한다. 반면에 1 fm이내의 짧은 거리에서는 양성자와 중성자간에 '중간자'(meson)라는 것이 매개하는 강한 핵력이 작용한다. 1934년 일본의 유카와 히데키(Hideki Yukawa)는 중간자의 존재를 이론적으로 유도하여 1949년 노벨 물리학상을 수상하였다.
스펙트럼선의 선폭 증가
자연 선폭 증가하이젠베르크(Werner Karl Heisenberg)의 불확정성 원리는 본래 주어진 상태의 에너지는 다음보다 더 정확하게 결정할 수 없다는 것을 말한다. 이는
로 표현할 수 있다. 이 방정식에서 h는 플랑크 상수이고, Δt는 상태 지속 시간이다. 따라서 원자의 집단이 만드는 흡수 또는 방출 스펙트럼선은 광자의 진동수가 퍼진 최소 선폭(자연선폭)을 가진다는 것을 의미한다. 일반적으로 들뜸 상태는 다시 가라앉기까지 약 10-8초 동안 지속되기 때문에 보통 자연선폭은 가시광선에서 5×10-5nm정도가 된다. 준안정 상태는 경우에 따라서 1초 이상 지속되므로, 이때는 훨씬 좁은 자연 선폭이 생기는 것을 볼 수 있다.
열적 도플러 선폭 증가
ΔE∙ Δt ≥ h/2π
로 표현할 수 있다. 이 방정식에서 h는 플랑크 상수이고, Δt는 상태 지속 시간이다. 따라서 원자의 집단이 만드는 흡수 또는 방출 스펙트럼선은 광자의 진동수가 퍼진 최소 선폭(자연선폭)을 가진다는 것을 의미한다. 일반적으로 들뜸 상태는 다시 가라앉기까지 약 10-8초 동안 지속되기 때문에 보통 자연선폭은 가시광선에서 5×10-5nm정도가 된다. 준안정 상태는 경우에 따라서 1초 이상 지속되므로, 이때는 훨씬 좁은 자연 선폭이 생기는 것을 볼 수 있다.
열적 도플러 선폭 증가는 기체의 온도와 화학 조성에 관련되는데 기체가 임의의 온도 T에 있을 경우, 기체 입자는 평균 운동 에너지 식에 따르는 맥스웰 속도 분포를 가진다.
원자 운동이 가지는 시선 방향 성분은 원자의 천이에서 흡수하거나 방출되는 복사에 도플러 이동을 일으키는데 주어진 온도에서, 무거운 원소의 스펙트럼선이 가벼운 원소의 스펙트럼선보다 더 가늘어지는 현상을 보인다. 그 이유는 무거운 입자가 일반적으로 가벼운 입자보다 느리게 움직이기 때문이다.
충돌 선폭 증가
원자 운동이 가지는 시선 방향 성분은 원자의 천이에서 흡수하거나 방출되는 복사에 도플러 이동을 일으키는데 주어진 온도에서, 무거운 원소의 스펙트럼선이 가벼운 원소의 스펙트럼선보다 더 가늘어지는 현상을 보인다. 그 이유는 무거운 입자가 일반적으로 가벼운 입자보다 느리게 움직이기 때문이다.
원자의 에너지 준위는 전자나 이온과 같은 이웃하는 전기를 띤 입자에 의하여 변화된다. 기체에서 이러한 교란은 무질서하게 발생하고, 이는 스펙트럼의 폭이 넓어지는 결과를 가져온다. 교란시키는 입자가 가까이 있을수록 교란은 더욱 커지며, 충돌 선폭 증가는 입자의 밀도에 의존된다. 즉, 밀도가 클수록 스펙트럼의 선폭은 넓어진다는 뜻이다.
그 밖의 선폭 증가로는 제만효과, 난류 선폭 증가, 팽창 선폭 증가, 회전 선폭 증가가 있다.
전달 방정식
그 밖의 선폭 증가로는 제만효과, 난류 선폭 증가, 팽창 선폭 증가, 회전 선폭 증가가 있다.
전달방정식이란 복사가 가스 구름이나 행성, 항성의 대기를 통과한 후 기대되는 복사의 세기를 계산한 미분 방정식을 말한다. 이들 방정식은 주로 천체들을 묘사하는데 사용 되었다.방정식을 보기에 앞서 몇 가지 양들을 알아야 하는데, 아래첨자 υ는 주파수에 의존되는 양을 말한다.
- 방출 계수 ηυ : 복사장에 추가된 에너지. 단위는 cm-3 sr-1 Hz-1 s-1.
- 원천 함수 sυ=ηυ/xυ : 총 불투명도에 대한 총 방출 비. 열역학적 평형의 경우 Sυ는 플랑크 분포 함수로 주어진다.
- 광학 깊이 : τυ는 시선 방향에 평균 자유 경로 길이의 수.
우선, 물리적 깊이의 요소 dl에 대한 미분방정식을 쓰면,
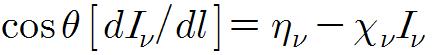
이다. 여기에 μ=cosθ로 정의 하고, xυ로 나누면 전달방정식의 표준형을 얻을 수 있다.
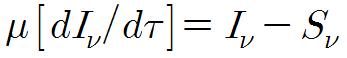
관측자가 천체 내부 방향으로 보는 경우를 나타내기 위해서 음의 기호(-)가 붙었다. 이것의 일반해를 구하면,
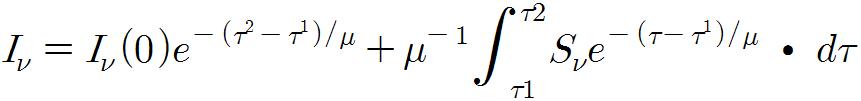
를 얻을 수 있다.
최종수정일
2017년 3월 31일

