모달창 닫기
운동량 보존의 법칙
- 홈으로 이동
운동량 보존의 법칙
질량이 m, 속도가 v인 입자의 경우 운동량(momentum)은 질량과 속도의 곱으로 정의한다. 운동량을 p라 하면,
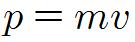
이다. 그리고 속도가 벡터 이므로 운동량도 벡터이다.
두 개의 입자가 상호 운동을 한다고 하면, 두 입자의 총 운동량 P는
두 개의 입자가 상호 운동을 한다고 하면, 두 입자의 총 운동량 P는
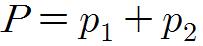
이 된다. 이처럼 총 운동량은 각 입자의 운동량의 벡터 합에 해당한다.
두 개 이상의 물체가 상호작용을 할 경우 운동량은 매우 중요한 개념이 되는데, 예를 들어 중력장 밖에서 두 개의 물체 사이에 힘이 작용하면, 뉴턴의 제 3법칙에 의해 두 힘은 언제나 크기는 같고 방향은 반대가 된다. 또 각 입자에 작용하는 힘은 운동량의 변화와 같으므로, 두 물체 사이의 운동량의 변화는 같고 방향은 반대가 된다. 결국 운동량의 변화는 0이고 총 운동량은 보존된다. 총 운동량의 시간적 변화율을 구해보면,
두 개 이상의 물체가 상호작용을 할 경우 운동량은 매우 중요한 개념이 되는데, 예를 들어 중력장 밖에서 두 개의 물체 사이에 힘이 작용하면, 뉴턴의 제 3법칙에 의해 두 힘은 언제나 크기는 같고 방향은 반대가 된다. 또 각 입자에 작용하는 힘은 운동량의 변화와 같으므로, 두 물체 사이의 운동량의 변화는 같고 방향은 반대가 된다. 결국 운동량의 변화는 0이고 총 운동량은 보존된다. 총 운동량의 시간적 변화율을 구해보면,
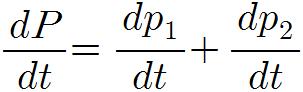
이고, 두 물체 사이에 작용하는 힘을 F1, F2로 하면, 뉴턴의 제 2법칙에 의해,
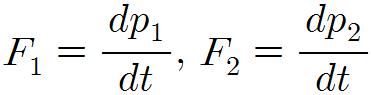
이다. 뉴턴의 제 3법칙에 의해 F1, F2 = 0 이므로,
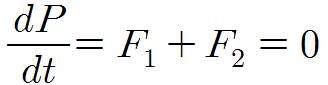
을 얻을 수 있다. 따라서 총 운동량의 시간에 따른 변화율은 0이다.
이를 통해, 계의 외력의 벡터 합이 0인 경우에는 언제나 계의 총 운동량은 일정하다는 것을 알 수 있다. 이것이 운동량 보존법칙이다. 이 원리를 유도하기 위해 뉴턴의 제 2법칙을 사용했으므로 관성계에서만 통용될 수 있다.
이를 통해, 계의 외력의 벡터 합이 0인 경우에는 언제나 계의 총 운동량은 일정하다는 것을 알 수 있다. 이것이 운동량 보존법칙이다. 이 원리를 유도하기 위해 뉴턴의 제 2법칙을 사용했으므로 관성계에서만 통용될 수 있다.
최종수정일
2017년 3월 31일

