모달창 닫기
- 홈으로 이동
라그랑지 역학
라그랑지 점(Lagrangian Point)
라그랑지(Joseph Louis Lagrange)는 18세기의 수학자겸 물리학자이다. 태양과 지구, 위성의 3체 문제 연구를 통하여 라그랑지 점을 발견했다.
라그랑지 점은 태양과 지구가 만들어낸 중력과 위성의 원심력이 상쇄되어 실질적으로 중력의 영향을 받지 않는 공간상의 어떤 지점을 의미한다. 라그랑지점에는 총 5곳이 있으며 각각 L1, L2, L3, L4, L5로 표기한다.
라그랑지 점은 태양과 지구가 만들어낸 중력과 위성의 원심력이 상쇄되어 실질적으로 중력의 영향을 받지 않는 공간상의 어떤 지점을 의미한다. 라그랑지점에는 총 5곳이 있으며 각각 L1, L2, L3, L4, L5로 표기한다.
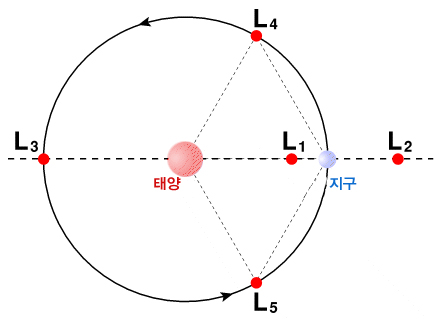
L1, L2, L3 라그랑지 점은 평형 점에 있던 물체들의 위치가 약간만 벗어나게 되면 원래 있던 평형 점으로 되돌아오지 못하는 불완전 평형점이고, L4, L5 라그랑지 점은 있던 물체들의 위치가 약간은 벗어난다고 해도 원래 있던 평형 점으로 되돌아오는 완전 평형점이다. 따라서 물체들은 자연스럽게 L4, L5 라그랑지 점으로 모이게 된다.
L1은 두 천체의 중력 평형 점으로 별의 진화에서 중요한 역할을 한다. 그리고 L4, L5는 외부 천체가 안정된 궤도를 유지하는 점으로 이곳에서는 소행성이 발견되는 경우가 많다. 이 중 지구에서 가까운 L2는 지구에 가려지지 않기 때문에 태양계 밖의 우주를 관측하기에 최적의 위치이다.
L2의 위치는 비교적 간단히 계산할 수 있다. 우선, L2는 태양과 지구를 잇는 연장선에 있으므로, x의 위치가 L2가 된다.
L1은 두 천체의 중력 평형 점으로 별의 진화에서 중요한 역할을 한다. 그리고 L4, L5는 외부 천체가 안정된 궤도를 유지하는 점으로 이곳에서는 소행성이 발견되는 경우가 많다. 이 중 지구에서 가까운 L2는 지구에 가려지지 않기 때문에 태양계 밖의 우주를 관측하기에 최적의 위치이다.
L2의 위치는 비교적 간단히 계산할 수 있다. 우선, L2는 태양과 지구를 잇는 연장선에 있으므로, x의 위치가 L2가 된다.
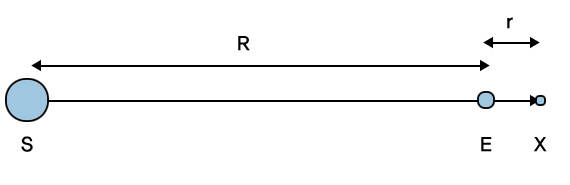
계산하기에 앞서 두 가지 조건을 고려해야 한다. 첫 번째, x가 받는 총 중력은 x가 뛰쳐나가려는 힘과 같다. 두 번째, x의 공전주기는 지구와 태양간의 공전주기와 같다.
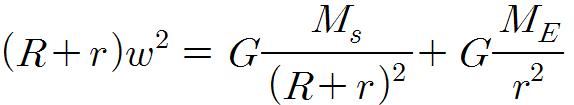
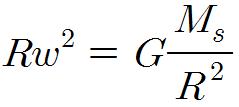
위 두식에서 회전각속도가 같으므로,
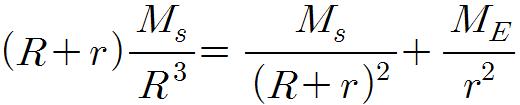
가 된다. 여기서 r은 R보다 매우 작으므로,
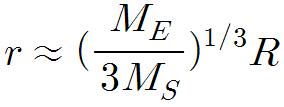
이와 같은 식을 얻을 수 있다.(Ms:태양질량, Me:지구질량 ω:회전각속도)
최종수정일
2017년 3월 31일

